Welcome to the Wonderful World of Fractals
![]()
This page will discuss the following topics: The history of fractals, the basic concept of fractals, frequently asked questions about fractals, and examples of some famous fractals. There will also be a list of links to some fractal web pages.
![]()
"I coined fractal from the Latin adjective fractus. The corresponding Latin verb frangere means 'to break' to create irregular fragments. It is therefore sensible - and how appropriate for our need ! - that, in addition to "fragmented" (as in fraction or refraction), fractus should also mean "irregular", both meanings being preserved in fragment." B. Mandelbrot
![]() ,
,
How long is the eastern coast of the US? There is certainly a defined length for it. However, "fractally" speaking, the length of the US eastern coast is infinity. Why? A person given a map of the US can sit down with a ruler and soon figure out the length. The problem is that repeating the process with a larger scale map leads to a greater estimate of length (Fig. 1). If the person actually went to the coast and measured them directly, even greater estimates would result. This fact shows that as the scale decreases, the estimated length increases without limit. Therefore, if the scale of the measurements were to be infinitely small, then the estimated length would become infinitely large!!!
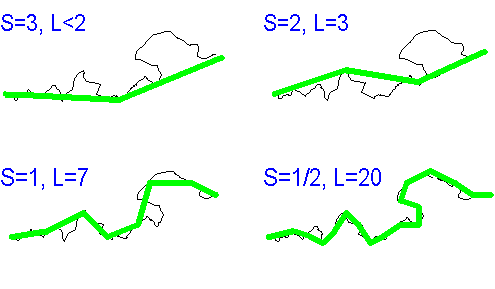
Fig. 1 This picture is showing that as the ruler gets smaller, the total length becomes longer.
Scale can be pictured in the mind as a measuring stick of a certain length. The finer the scale, the shorter the stick. Thus at any scale, think of a curve as being represented by a sequence of sticks (Fig. 1), joined end-to-end. Clearly, any feature shorter than the stick will not be shown from a map constructed this way. Of course, I don't think that anyone actually makes maps by laying sticks on the ground, but the stick analogy shows that the distortions are inevitably produced by the human eye, by the limited resolution of photographs, or even by the thickness of the pens used in drafting.
Mandelbrot proposed the idea of a fractal (short for "fractional dimension") as a way to cope with problems of scale in the real world. He defined a fractal to be any curve or surface that is independent of scale. This property, referred to as self-similarity, means that any portion of the picture, if blown up in scale, would appear identical to the large picture.

Fig. 2. Forming a cross by iteration of a simple procedure.
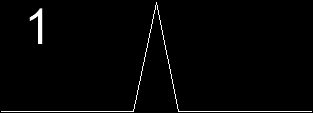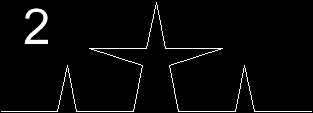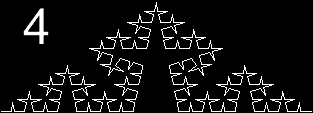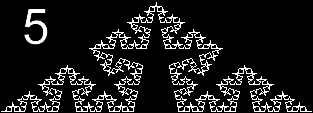
This is an animated picture of a simple fractal.
![]() ,
,
The first fractals were found during the 19th century. Cantor's dust created in 1872 is probably the most ancient known fractal. In 1890, Peano published his famous curve. Koch's curve was published in 1904. Then came Sierpinski's triangle in 1915. A few mathematicians noticed that there were more sophisticated means to define the dimension of an object. Fundamental work was done by Hausdorff (1919), then developed by Besicovitch (1935). The Hausdorff-Besicovitch dimension has played , later on, a major role in the domain of fractals.
Everything mentioned above was well known before Mandelbrot's works, but these were scattered elements, and only understood by a small number of specialists. Therefore little attention had been paid to this knowledge and no one had thought of bringing together all theses elements. Mandelbrot's brought the ideas together and to develop an entirely new mathematical domain. The term self-similar seems to have appeared for the first time in 1964, in an internal report at IBM (where Mandelbrot was doing research) and in the title of a 1965 paper. The acceptance of the word fractal was dated in 1975. When people read the list of Mandelbrot's publications between 1951 and 1975, date when the French version of his book was published, they were astonished by the variety of the studied fields : noise on telephone lines, games theory, linguistics, economy, cosmology, turbulence, etc. The multiplicity of his fields of interest has undoubtedly played a key role in the genesis of his discovery.
Mandelbrot was then interested in noise on telecommunications lines, in turbulence, in geophysical problems such as the length of coastlines, in the hydrologic regime of streams that were badly described with the theories known at that time. In all these cases, he was capable of applying the same mathematical approach and he found every time the notion of self-similarity.
 Peano
Peano
 Koch
Koch  The Sierpinski's
The Sierpinski's
![]() ,
,
 |
 |
 |
|---|---|---|
 |
 |
 |
 |
 |
 |
![]() ,
,
Fractal World

![]()
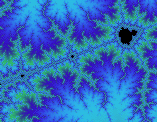
Julia Set

![]()
Web page created by James Sun
Last Updated: 03/12/98